When I was in the high school learning about AP statistics I learned the formula:

$$ P(A|B)=\frac{P(A\cap B)}{P(B)} , P(B|A)=\frac{P(A\cap B)}{P(A)}$$

Which able to be transformed as:

$$ P(A\cap B)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B) $$

$P(A|B)$ is called “Conditional probability” which pretty much self-explained itself. For which I only knew the meaning of each element but not the whole idea, what I do is just plug in numbers, because it is kinda abstract to understand from itself: “The probability of event $A$ happens given event $B$ happened = The probability of events $A and B$ happens divided by the probability of event $B$ happens”

Before we talking about the Bayes’ Rule, I want to discuss why the conditional probability satisfies such a relationship:

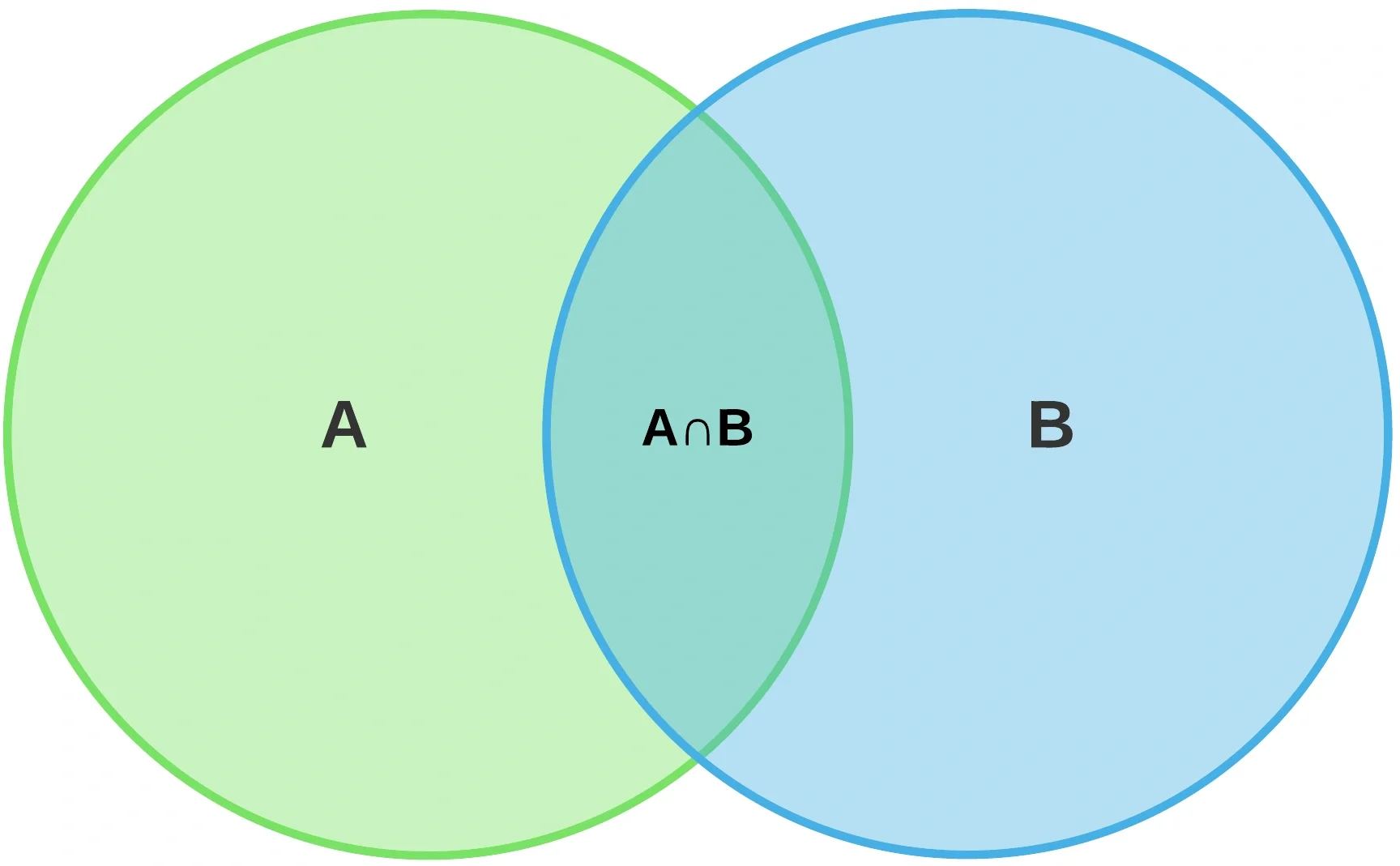
For the Venn diagram showing above, the outer space represents the whole sample space. When we want to know $P(A|B)$, which by definition: the probability of $A$ while $B$ is true. Naturally, we can find that the portion makes $A$ true in circle $B$—$A\cap B$, then divided it by $B$—$\frac{P(A\cap B)}{P(B)}$. So the latter $B$ restricts the space into that blue circle $B$, and what we do is just find the part in which $A$ is true.

For people who dig deep, they might ask: “That’s can’t be right, $A$ and $B$ are just samples, they are not probabilities, so the formula did above does not match!” Well, the fact is we did omit a little about the sample space, for which we call it $S$. What we saying “probability” is actually, using $A$ as an example, $P(A)=\frac{A}{S}$. And the S would be canceled out, so I omit a little and directly using the $A$&$B$ portion in the diagram.

$$P(A|B)=\frac{ P(B|A) }{P(B)}\cdot P(A)$$

So, what should the Bayes’ Rule mean?

Base on the formula, it is asking the probability of event $A$ to happen with the restriction of the event $B$. The formula itself could be easily derived from the conditional probability formula. And here we focus on how to interpret it.

The basic idea of the Bayes’ Rule is to adjust the general probability, in this case, we say $P(A)$, by a parameter $\frac{P(B|A)}{P(B)}$ to gain a better idea of $P(A)$ with a restriction, or a piece of new evidence, $B$, and be called as $P(A|B)$

More related equations:

$$P(B)=\sum_{i=1}^{n}P(B|A_{i})\cdot P(A_{i})$$