Foundations of Machine Learning II
The least squares estimates of α and β⌗
For simple linear regression:
$$ E\left ( Y|X=x \right ) = \alpha +\beta x $$
we have:
$$ \hat{\beta } = \frac{cov\left ( X, Y \right )}{var\left ( X \right )} $$
$$ \hat{\alpha} = \bar{Y} - \hat{\beta}\bar{X} $$
Linear Regression way⌗
We can all use the NN method to solve the regression problem but that leads to being nearly impossible to locate exactly which layer foreshadows which feature of the data. Thus, maybe the better way is to upscale the dimension of the linear regression method. That, we not only use $ x $ but $x, x^{2}, x^{1/2}… $to approach the true curve.
Classification method⌗
Parametric methods:⌗
Direct way = $ E\left ( Y|X=x \right ) = Sigmoid(\beta ^{T}X) $
Bayes way *TODO:needs elaboration
Nonparametric methods:⌗
KNN *TODO:needs elaboration
Elastic Net *TODO:needs elaboration
PCA *TODO:needs elaboration
Spline *TODO:needs elaboration⌗
Local Regression *TODO:needs elaboration⌗
Tree Methods *TODO:needs elaboration⌗
Convex Analysis&Optimization⌗
For the case of convex data, it is very easy to find the minimal(global), but for the case of non-convex data, the situation would be a little complex. To analysis such a situation, we need to discuss it under different assumptions.
Lipschitz continuous⌗
Definition, for all $x_{0}, x_{1}$:
$\left | f(x_{0})-f(x_{1}) \right |\leq L(|x_{0}-x_{1}|)$
For the purpose of clearance, we would use 2-dimensional space.
If the function is only Lipschitz continuous, then even it could varies in a certain range but it is not smooth, so we cannot apply gradient descent.
Let’s define a domain $[0,1]$, and we can divide the domain in to $k$ cuts, so the cutting points are: $\frac{1}{k}, \frac{2}{k},…,\frac{k}{k}$, and know the target is $\chi \in [\frac{i}{k}, \frac{i+1}{k}]$
Now, how about the distance $\chi -\frac{i}{k}|$? Since we assume the function is lipschitz continuous, and each cut is $\frac{1(,or L)}{k}$, then we have $|f(\chi) -f(\frac{i}{k})|\leq L|\chi -\frac{i}{k}| \leq \frac{L}{k}$
And we have a concept called tolerance, $\epsilon$, which talks about the precision of the result you want, for example, 1e-6.
*TODO: Here remains a question
Definition:
$$ \left | \bigtriangledown f(x_{0})-\bigtriangledown f(x_{1}) \right |\leq \left | x_{0}-x{1} \right | $$
Which is equivalent to:
$$ f(y)\leq f(x)+\bigtriangledown f(x)^{T}(y-x)+\frac{L}{2}\left | y-x \right |_{2}^{2} $$
So such assumption implies a certain relationship between $f(y)$ and $f(x)$
Convexity⌗
Set Convexity
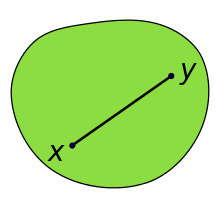 convex set G |
 non-convex set G |
|---|
Function Convexity
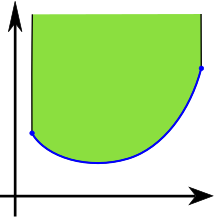
convex function f(G)
“A function is convex if and only if its epigraph, the region (in green) above its graph (in blue), is a convex set.”
So for a convex function, there would only be one local, which is the global, minimum.
The Convergence rate of Gradient Descent⌗
Suppose the function $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ is convex and differentiable, and that its gradient is Lipschitz continuous with constant L > 0, i.e. we have that $\left | \bigtriangledown f(x_{0})-\bigtriangledown f(x_{1}) \right |\leq \left | x_{0}-x_{1} \right |$ for any x, y. Then if we run gradient descent for k iterations with a fixed step size $t ≤ \frac{1}{L}$, it will yield a solution $f(k)$ which satisfies:
$$f(x^{(k)})-f(x^{*}) \leq \frac{\left | x^{0}-x^{*} \right |_{2}^{2}}{2tk}$$
Such expression implies how it guarantees improvement(converge)
Epochs to run:
$$\frac{1}{\epsilon}$$
TODO: USE LOG?