Foundations of Machine Learning III
The Primal Question of Optimization⌗
For a general optimization problem, it usually could be rewritten as maximizing or minimizing a certain function with several constrictions. For example, maybe you want the optimized value non-negative. The most basic form of such is called the primal question which looks like this:
$$ \begin{matrix} \underset{x}{min}f(x), x \in \mathbb{R}^n \newline s.t. \newline g_i(x)\leq 0, i=1,2,…,m \newline h_i(x)= 0, i=1,2,…,p \end{matrix} $$
And we call $f(x)$ the objective function and the rest two the constriction function.
The Lagrangian Function⌗
To solve such primal question with constrictions, we can use the Lagrange multiplier to encode the three functions into one:
$$ L(x,u,v)=f(x)+\sum_{i=1}^{m}u_ig_i(x)+\sum_{i=1}^{m}v_ih_i(x) $$
As such, we call $u_i,v_i$ the lagrange multipliers.
And we make $u_i \geq 0, v_i \in \mathbb{R}$ so that:
Because $g_i(x) \leq 0$, so that the maximum of $\sum_{i=1}^{m}u_ig_i(x)$ is 0. And since $h_i(x)=0$, so $\sum_{i=1}^{m}v_ih_i(x)$ is also equal to 0. Thus:
$$\underset{u,v}{max}L(x,u,v)=f(x)+0+0=f(x)$$
In this way, we find:
$$\underset{x}{min}f(x)=\underset{x}{min}\underset{u,v}{max}L(x,u,v)$$
The Lagrangian Dual Function⌗
But we find the expression above is hard to solve, so we need to transfer it to a dual function as such:
Define $D$ the feasible domain:
$$g(u,v)=\underset{x\in D}{inf}L(x,u,v)=\underset{x\in D}{inf}[f(x)+\sum_{i=1}^{m}u_ig_i(x)+\sum_{i=1}^{m}v_ih_i(x)]$$
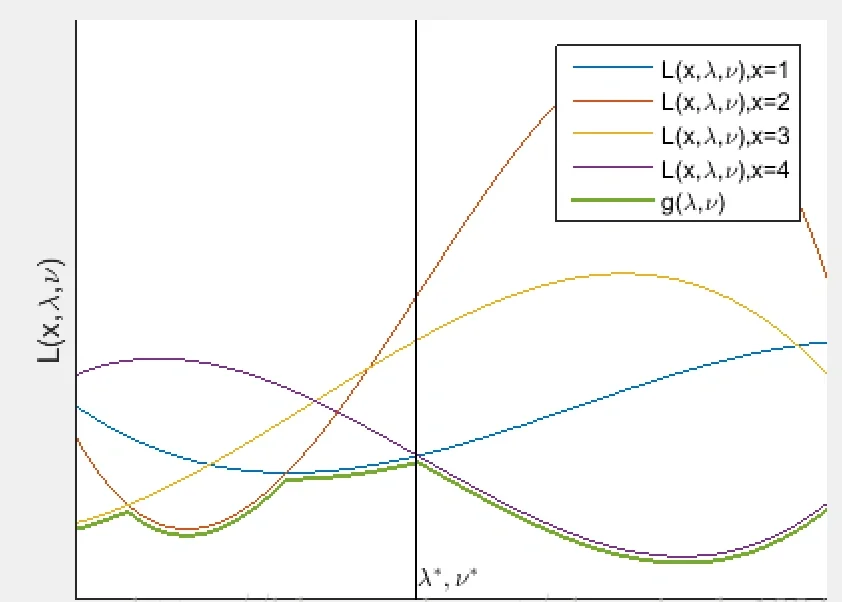
while the function does not have a lower bound, we define the value as $-\infty$, so that the dual is a concave function, and since we are trying to find the maximum, it could be treated as a convex optimization problem.
Because:
$$\underset{x}{min}f(x)=\underset{x}{min}\underset{u,v}{max}L(x,u,v)\geq \underset{u,v}{max}\underset{x}{min}L(x,u,v)= \underset{u,v}{max}g(x)$$
Proof of the Minimax Theorem⌗
Dual gap⌗
we use $p^*$ to represent the optimized solution of the primal problem:
$$p^*=\underset{x}{min}f(x)$$
And $d^*$ to represent the optimized solution of the lagrangian dual:
$$d^*=\underset{u,v}{max}g(u,v)$$
And because the minimax theorem:
$$p^* \geq d^*$$
We are using $ d^* $ to approach $ p^* $ and calling $ p^* - d^* $ the dual gap
When the dual gap is zero, we call the situation as strong dual, otherwise the weak dual.
I am not going to write about KKT&Slater for now…*